O.B.d.A., wir, kommutatives Diagramm |Mathematik Studium Tipps

Mathematiker benutzen nicht nur ihre eigenen Symbole und Buchstaben. Sie verwenden auch eigene mathematische Begriffe.

Diese Vokabeln sehen deutsch aus. Doch ihre Bedeutung weicht entweder von dem umgangssprachlichen Verständnis ab oder sie sind in unserem deutschen Alltagswortschatz nicht enthalten.

Dieser Beitrag ist der zweite einer vierteiligen Serie. Wir betrachten

Ich, wir, man,
Kommutatives Diagramm,
O.B.d.A., o.B.

Dazu erhälst du eine Übersetzung oder Erklärung. Beispiele runden den zweiten Teil unseres kleinen Sprachkurses schließlich ab.

Ich, wir, man

Im schriftlichen Wortschatz eines Mathematikers findest du kein „ich“. Der Mathematiker schreibt entweder „wir“ oder „man“.

Er verwendet „wir“, wenn er den Leser aktiv mit einbinden möchten. Das bedeutet der Leser ist zum Mitdenken aufgefordert. Das „wir“ wird daher gerne in Beweisen benutzt. Typische Satzanfänge sind:

Wir betrachten …

Wir nehmen an, …

Wir müssen zeigen, dass …

Damit haben wir gezeigt, dass …

Das „man“ dagegen findet Einsatz, wenn etwas nicht aktiv nachvollzogen werden braucht. Es geht dann rein um die Information. Beispiele sind hier

In der Literatur findet man …

In der Mathematik verwendet man häufig …

… bezeichet man auch als …

Bei einem „wir“ solltest du dich immer angesprochen fühlen und versuchen mitzudenken. Ansonsten wirst du schnell abgehängt und verstehst gar nichts mehr.

Kommutatives Diagramm

Kommutative Diagramme findest du häufiger in der (Linearen) Algebra als in der Analysis. Schauen wir uns doch direkt mal zwei Beispiele dazu an.

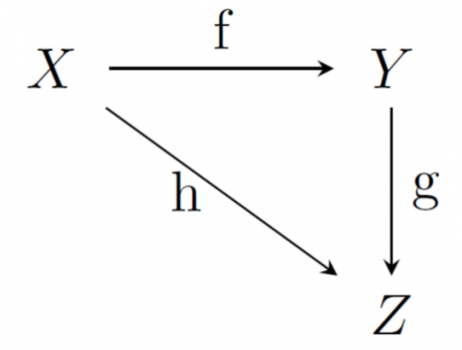
Das Diagramm links ist aus der Analysis und beschreibt drei Funktionen $(f,g,h)$ und ihre Definitions- sowie Wertebereiche $(X,Y,Z)$ . Die Besonderheit an den Funktionen ist, dass der Wertebereich $Y$ von $f$ wiederum der Definitionsbereich $Y$ von $g$ ist. Die Menge $Z$ ist sowohl von Funktion $g$ als auch von Funktion $h$ der Wertebereich.

Damit haben wir erst einmal das Diagramm beschrieben. Offensichtlich gibt es zwei Möglichkeiten, um Elemente der Menge $X$ auf Elemente der Menge $Z$ abzubilden. Wir können beide Wege im Diagramm benutzen. Daher sagen wir auch, das Diagramm kommutiert.

Da $h=f\circ g$ , kommutiert das Diagramm.

Das mathematische Symbol $\circ$ steht hier für eine Verknüpfung oder auch Verkettung von Funktionen.

Ein typisches kommutatives Diagramm aus der lineare Algebra ist das nachfolgende. Es beschreibt die Beziehung zwischen vier Abbildungen $(T, \Psi, A, \Phi)$ und ihren Definitions- und Wertebereichen $(V, W, \mathbb{R}^m, \mathbb{R}^n)$ .

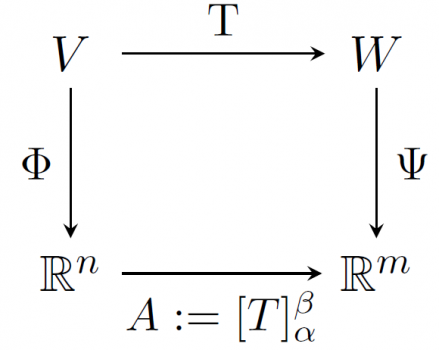
Auch hier kommutiert das Diagramm. Denn wir können $\Phi$ und $A$ verketten, um nach $\mathbb{R}^m$ abzubilden. Alternativ können wir aber auch $T$ und $\Psi$ verketten und bilden dadurch auch nach $\mathbb{R}^m$ ab.

Im kommutativen Diagramm gilt $\Phi \circ A = T\circ \Psi$ .

Somit zeigt ein kommutatives Diagramm einfach nur, dass mehrere Wege zum Ziel führen.

O.B.d.A., o.B.

Die Langformen zu den Abkürzungen o.B.d.A. und o.B. sind „ohne Beschränkung der Allgemeinheit“ und „ohne Beschränkung“. Obwohl sie länger ist, wird die erste Version häufiger verwendet als die zweite. In ihrer Bedeutung unterscheiden sie sich nicht.

Typischerweise findest du die beiden Abkürzungen in Beweisen zu mathematischen Aussagen. Wann es Sinn macht o.B.d.A. einer Annahme voranzustellen wollen wir uns anhand von Beispielen deutlich machen.

Sei $r\in \mathbb{N}$ die Anzahl linear abhängiger Spalten der Matrix $A$ . O.B.d.A. seine die ersten $r$ Spalten $a_1, \ldots, a_r$ linear unabhängig. …

Warum können wir hier annehmen, dass in der Matrix genau die ersten $r$ Spalten schon linear unabhängig sind?

Der Gedankengang ist hier im Grunde ganz einfach: Wären nicht bereits schon die ersten $r$ Spalten linear unabhängig, dann könnten wir doch einfach die Spalten entsprechnd umsortieren. Mit o.B.d.A. setzen wir also lediglich voraus, das das Umsortieren schon geschehen ist.

Der Vorteil dieser Vorgehensweise liegt darin, dass eine Bündelung in Form von „die ersten r Spalten“ die Bezeichnung der linear unabhängigen Spalten für die weitere Beweisführung erleichtert.

Für $a,b\in \mathbb{R}_+:\ |\frac{a}{b}+ \frac{b}{a}|\ge 2$ . Beweis: O.B.d.A. sei $a\neq b$ . …

In dem vorangegangenen Beispiel wird o.B.d.A. verwendet, um auf triviale Spezialfälle nicht weiter eingehen zu müssen. Denn für triviale Spezialfälle gilt die zu beweisende Aussage, ohne dass irgendetwas besonderes zu zeigen ist.

Für unser Beispiel bedeutet das: Ist $a=b$ , dann folgt aus der Unleichung stets eine Gleichung. Daher konzentrieren wir uns im Beweis auf die Fälle $a\neq b$ und kürzen mit der Einleitung „o.B.d.A.“ den Beweis ein wenig ab.

Das letzte Beispiel macht deutlich, dass die Betrachtung eines Spezialfalles aber auch zur Vereinfachung des Beweises führen kann.

Es gibt genau $n!$ bijektive Abbildungen einer $n$ -elementigen Menge $A$ in eine $n$ -elementige Menge $B$ . Beweis: Sei o.B.d.A. $A = B$ . Dann ist die gesuchte Anzahl gleich der Anzahl der Permutationen von $A$ , also gleich $n!$ .¹⁾Beutelspacher, A. (2009): „Das ist o.B.d.A. trivial!“, Tipps und Tricks zur Formulierung mathematischer Gedanken, Wiesbaden.

Wichtig für die Aussage ist lediglich, dass beide Mengen gleich viele Elemente enthalten. Da die Mengen abzählbar viele Elemente enthalten, können wir sowohl in $A$ als auch in $B$ diese Elemente durchnummerieren.

Jedes Element bekommt also eine neue Beschriftung. Dadurch erhalten wir zwei Mengen, die jeweils $n$ Elemente enthalten, durchnummeriert von $1, 2, \ldots, n$ .

Dadurch unterscheiden sich die Mengen A und B nicht mehr. Wir können also ohne Beschränkung annehmen, dass $A = B$ gilt und den Beweis unter dieser Annahme führen.

Die drei Beispiele machen deutlich, dass es mehrere Anwendungsmöglichkeiten für „o.B.d.A.“ gibt. Alle vereinfachen letztendlich den Beweis. Entweder wird die weitere Bezeichnung von Objekten erleichtert, der Beweis um triviale Spezialfälle verkürzt oder der Beweis wird durch die Reduktion auf einen speziell aussehenden Fall, der aber tatsächlich alle anderen Fälle einschließt, ebenfalls einfacher.