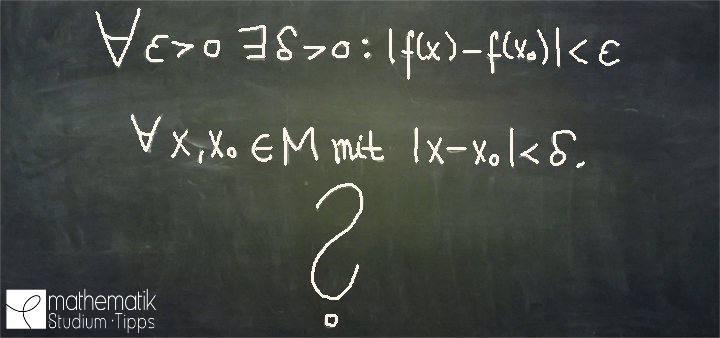Mathematische Symbole: Hier die Wichtigsten

Mathematik ist eine Sprache, die du wie jede Sprache erst einmal erlernen musst bevor du in ihr kommunizieren kannst. Die Mathematik hat ihre eigenen Vokabeln, Buchstaben und vor allem eigene mathematische Symbole.

Gerade mathematische Symbole gibt es unzählige.

Welche mathematischen Symbole insbesondere im ersten Semester deines Mathematikstudiums wichtig für dich sind, fasst dieser Beitrag zusammen.

Mathematische Symbole – Grundlagen

Symbol	Bezeichnung	Sprechweise	Verwendung
${\color{gray}A}\neg$	Negation	nicht	$\neg A$
${\color{white}A}\wedge$	Konjunktion	und	$A \wedge B$
${\color{gray}A}\vee$	Disjunktion	oder	$A \vee B$
${\color{white}A}\exists$	Existenzquantor	Es gibt (mindestens) ein	$\exists\ n \in \mathbb N$
${\color{gray}A}\exists !$	Existenzquantor	Es gibt genau ein	$\exists !\ n \in \mathbb N$
${\color{white}A}\nexists$	Existenzquantor	Es gibt kein	$\nexists\ n \in \mathbb N$
${\color{gray}A}\forall$	Allquantor	Für alle	$\forall\ \varepsilon\ \textgreater\ 0$
${\color{white}A}\Rightarrow$	Implikation	Aus … folgt …	$A \Rightarrow B$
${\color{gray}A}\Leftrightarrow$	Äquivalenz	äquivalent zu … genau dann, wenn …	$A \Leftrightarrow B$
${\color{white}A}\text{:}\Leftrightarrow$	Definitionsäquivalenz	ist definitionsgemäß äquivalent	$E:\Leftrightarrow\ B$
${\color{gray}A}\text{:=}$	Definitionsgleichheit	ist definiert als	$M:=\lbrace 2, 4, 6, 8, 10, \ldots\rbrace$
${\color{white}A}\text{:}$	—	so dass	$\forall\ x \in M\ \exists\ q \in \mathbb{N}\ : x = 2q.$
${\color{gray}A}\equiv$	—	… identisch … oder … kongruent …	$\sin^2 (x) + \cos^2(x) \equiv 1$ $12 \equiv 27\ \text{mod}\ 5$

Die mathematischen Symbole $\neg,\ \wedge,\ \vee$ kommen aus der Logik. Dort werden sie am meisten verwendet. Zu Beginn deines Mathematikstudiums spielt die Logik eine wichtige Rolle, da du sie während des gesamten Studiums – wenn auch eher indirekt – bei der Beweisführung brauchen wirst.

Die Negation, Konjunktion und Disjunktion brauchst du schon für dein erstes Übungsblatt. Die Symbole setzt du direkt in deinen ersten Beweisen zu Aussagen der Mengenlehre ein.

Hervorzuheben ist hier, dass $\vee$ das „logische oder“ beschreibt. Das „logische oder“ bedeutet nicht „entweder … oder ….“ sondern schließt das „und“ mit ein.

Sind beispielsweise $A, B$ Aussagen, die wahr oder falsch sein können, dann bedeutet $A \vee B$ : $A$ ist wahr oder $B$ ist wahr. Eine der Aussagen kann somit falsch sein. Die Betonung liegt hier auf kann. Der Ausdruck $A \vee B$ schließt nicht aus, dass $A$ und $B$ wahr sind.

Die Quantoren $\exists,\ \exists !, \nexists,\ \forall$ dagegen werden dich während deines gesamten Studiums begleiten. Ich behaupte sogar:

Es wird kein Studientag ohne Quantoren vergehen!

Im Umgang mit Quantoren ist insbesondere die Negation von Quantoren ist wichtig, um Widerspruchsbeweise führen zu können.

Implikationspfeile und Äquivalenzpfeile wirst Du genauso wie das Definitionszeichen := und den Doppelpunkt : (der auch als „gilt“ gelesen werden kann) sicher täglich benutzen.

Beim Definitionszeichen steht der Doppelpunkt in := stets auf der Seite, auf der das zu definierende Objekt steht.

Etwas seltener wirst du das Zeichen $:\Leftrightarrow$ für Definitionsäquivalenz sehen. Ein Beispiel für seine Verwendung ist folgendes:
$X$ ist auf $\Omega$ $\mu$ -fast überall endlich $:\Leftrightarrow\quad \mu(\lbrace X=+\infty\rbrace\bigcup\lbrace X=-\infty\rbrace)=0$ .

Das Zeichen $\equiv$ steht für die Identität oder Kongruenz von zwei Ausdrücken. Es wird beispielsweise im Zusammenhang mit Gleichungen benutzt, die für alle möglichen Parameterwerte erfüllt sind.

Ein Beispiel ist: $\sin^2 (x) + \cos^2(x) \equiv 1$ . Allerdings wird das Identitätszeichen für diese Gleichung nicht so häufig angewendet. Meistens wird dann das normale Gleichheitszeichen verwendet.

Wenn mit $\equiv$ eine Kongruenz beschrieben wird, dann sieht das beispielsweise so aus: $12 \equiv 27\ \text{mod}\ 5$ . Du sprichst: 12 ist kongruent zu 27 modulo 5. Beide Zahlen ergeben den Rest 2, wenn du sie durch 5 teilst. Daher sind sie kongruent zueinander.

Konkrete Zahlen spielen während deines Mathematikstudiums höchstens in Form deiner Noten eine Rolle.

Statt einzelner Zahlen sind mathematische Symbole für ganze Mengen von Zahlen wichtig für dich. Du solltest mit den Symbolen $\mathbb{N}, \mathbb{Z}, \mathbb{Q}, \mathbb{R}, \mathbb{C}$ und den Mengen, die sie definieren, vertraut sein.

Mathematische Symbole – Zahlenmengen

Symbol	Bezeichnung	Beschreibung
${\color{white}A}\mathbb{N}, \mathbb{N}_0$	Menge der natürlichen Zahlen (ohne oder mit Null)	$\mathbb{N}=\lbrace 1, 2, 3, 4, 5, 6, \ldots \rbrace$ $\mathbb{N}_0=\mathbb{N}\cup \lbrace 0 \rbrace$
${\color{gray}A}\mathbb{Z}$	Menge der ganzen Zahlen	$\mathbb{Z} = \lbrace \ldots, -2, -1, 0, 1, 2, \ldots \rbrace$
${\color{white}A}\mathbb{Q}$	Menge der rationalen Zahlen	$\mathbb{Q} = \lbrace \frac{n}{m}\| n, m \in \mathbb{Z} \wedge m\neq 0\rbrace$
${\color{gray}A}\mathbb{R}$	Menge der reellen Zahlen	$\mathbb{Q}\ \cup$ {irrationale Zahlen, z.B. $\pi, \sqrt{2}, e$ }
${\color{white}A}\mathbb{C}$	Menge der komplexen Zahlen	$\mathbb{C} = \lbrace a + b i \| a, b \in \mathbb{R}\rbrace$ , wobei $i:= \sqrt{-1}$
${\color{gray}A}M_+$	Menge der positiven Zahlen aus M	$M_+ = \lbrace x\in M \| x \ge 0 \rbrace$
${\color{white}A}M_-$	Menge der negativen Zahlen aus M	$M_- = \lbrace x\in M \| x < 0 \rbrace$

Typischerweise wirst du in den ersten beiden Semestern deines Mathestudiums die Eigenschaften der obigen Zahlenmengen studieren. Dazu wirst du Grundlagen der Gruppen-, Ring- und Körpertheorie kennenlernen.

Diese Grundlagen stammen aus der abstrakten Algebra. Mit ihrer Hilfe ordnest du den Zahlenmengen algebraische Strukturen zu, also bestimmte algebraische Eigenschaften.¹⁾Zahlenmengen können neben den algebraischen Strukturen auch Ordnungsstrukturen und topologische Strukturen besitzen, die alle miteinander verbunden sind.

Deine ersten beiden Vorlesungen im ersten Semester werden Analysis I und Lineare Algebra I sein. In beiden Veranstaltungen ist es üblich, dass die ersten Übungsaufgaben zur Mengenlehre gestellt werden, bevor du dich mit den Zahlenmengen als spezielle Mengen beschäftigst.

Die nachfolgenden mathematischen Symbole wirst du für die Mengenlehre benötigen.

Mathematische Symbole – Mengen

Symbol	Bezeichnung	Sprechweise	Verwendung
${\color{white}A}\in$	—	… Element in … alternativ … aus …	$x\in X$
${\color{gray}A}\notin$	—	… nicht Element in … alternativ … nicht aus …	$x\in X, \text{aber}\ x\notin Y$
${\color{white}A}\lbrace \ldots\rbrace$ , ${\color{white}A}\lbrace \ldots \| \ldots \rbrace$ , ${\color{white}A}\lbrace \ldots : \ldots \rbrace$	Mengenklammern	Die zweite und dritte Schreibweise liest sich: Menge aller …, für die gilt …	$\lbrace 13, 2, 7, 5, 17, 3\rbrace$ , $\lbrace n\in \mathbb{N}\ \|\ \text{n ist gerade}\rbrace$ , $\lbrace n\in \mathbb{N}\ :\ \text{n ist gerade}\rbrace$
${\color{gray}A}\lbrace \rbrace,$ ${\color{gray}A} \emptyset$	Leere Menge	… ist leer	$M= \emptyset$ , $M=\lbrace \rbrace$
${\color{white}A}\subset, \subseteq, \subsetneq$	Inklusion	… Teilmenge von …	$A\subset B$
${\color{gray}A}\cap$	Durchschnitt	… geschnitten …	$A \cap B$
${\color{white}A}\cup$	Vereinigung	… vereinigt …	$A \cup B$
${\color{gray}A}\dot{\cup}$	Disjunkte Vereinigung	… disjunkt vereinigt …	$A \dot{\cup} B$
${\color{white}A}\backslash$	Differenz	… ohne …	$A \backslash B$

Mengen werden in einfachen Fällen dadurch definiert, dass ihre Elemente als ungeordnete Liste in geschweifte Klammern gesetzt werden. Hier ein Beispiel einer einfachen Menge: $M:=\lbrace 13, 2, 7, 5, 17, 3\rbrace$ .

Alternativ kannst du eine Menge auch in dieser Form definieren: $N:=\lbrace n\in \mathbb{N}\ |\ \text{n ist gerade}\rbrace$ . Die Definition der Menge $N$ sprichst du so: $N$ ist die Menge aller natürlichen Zahlen $n$ , für die gilt, dass $n$ eine gerade Zahl ist.

Mit Mengen kannst du auch „rechnen“. Typische Mengenoperationen sind der Durchschnitt, die Vereinigung und die Differenz. Hierbei ist die disjunkte Vereinigung ein Spezialfall der Vereinigung im Allgemeinen. Zwei Mengen $A, B$ sind disjunkt, wenn $A \cap B = \emptyset$ , also wenn sie keine gemeinsamen Elemente haben.

Das Zeichen $\emptyset$ für die leere Menge wirst du in deinem Mathematikstudium häufiger benutzen als $\lbrace \rbrace$ .

Beide Symbole $\wedge$ und $\vee$ aus der Grundlagen-Tabelle werden nicht nur für Aussagen sondern auch für Elemente einer Menge wie $a\in A$ und $b\in B$ verwendet. Ein Beispiel ist: $A \cap B:=\lbrace x :\ x\in A \wedge x\in B\rbrace$ . Dieser Ausdruck ließt sich: $A$ geschnitten $B$ ist die Menge aller $x$ , für die gilt, $x$ ist Element in $A$ und $x$ ist Element in $B$ .

Ob du in den geschweiften Klammern lieber : oder | benutzt ist Geschmacksache. Beide mathematischen Symbole haben die selbe Bedeutung, nämlich „so dass“ oder auch „gilt“. Typischerweise werden Großbuchstaben für Mengen gewählt und Kleinbuchstaben für die Elemente einer Menge.

Ist eine Menge $A$ in einer anderen Menge $B$ enthalten, dann benutzt du das Inklusionszeichen. Hier gibt es drei Varianten. Leider werden sie nicht einheitlich verwendet.

Im Allgemeinen gilt für eine Teilmenge $A$ von $B$ , dass $A \subseteq B$ . Das bedeutet, dass auch $A = B$ möglich ist. Handelt es sich bei $A$ jedoch um eine echte Teilmenge, dann schreibst du $A \subset B$ oder $A \subsetneq B$ . Es gibt nun auch Mathematiker, die $A \subset B$ schreiben, wenn $A = B$ erlaubt ist.

Neben den speziellen Eigenschaften, die Mengen so haben können, interessiert den Mathematiker auch immer welche Abbildungen die Eigenschaften der Mengen (auch mathematische Strukturen genannt) erhalten.

Daher spielen Abbildungen von Beginn deines Mathematikstudiums an eine sehr wichtige Rolle.

Mathematische Symbole – Abbildungen

Symbol	Bezeichnung	Sprechweise	Verwendung
${\color{white}A}\mapsto$	Zuordnungspfeil	… wird abgebildet auf …	$x\ \mapsto\ f(x)$
${\color{gray}A}\to$	—	… von … nach …	$f:\ D \to W$
${\color{white}A}\circ$	Komposition, Verknüpfung oder Verkettung	… Kringel … … verknüpft mit …	$f\circ g: D \to W$
${\color{gray}A}f^{-1}$	Umkehrabbildung oder inverse Abbildung von f	Die inverse Abbildung von …Alternativ:… hoch minus 1	$f^{-1}:\ W \to D$
${\color{white}A}f^{-1}$	Urbild von f	Das Urbild der Menge … unter der Funktion…	$f^{-1}(W)=\lbrace x \in D\| f(x) \in W\rbrace$

Eine Abbildung $g: X \to Y,\ x \mapsto g(x)$ verändert ein Element $x\in X$ , so dass es nach der Veränderung ein Element $y:=g(x) \in Y$ ist. Was genau mit $x\in X$ geschieht, wird in der Abbildungsvorschrift $g(x)$ beschrieben, beispielsweise so: $g(x) := x +1$ .

Die obige Beschreibung der Abbildung g liest sich so: g von X nach Y mit x abgebildet auf g(x) definiert als x + 1.

Je weiter du fortschreitest in deinem Studium, desto weniger spielt die konkrete Abbildungsvorschrift (so wie x + 1) eine Rolle. Die Eigenschaften einer Abbildung sind meistens schon völlig ausreichend, um eine mathematische Aussage zu beweisen.

Die Menge links von dem Pfeil $\to$ wird allgemein als Definitionsbereich der Abbildung bezeichnet, die Menge rechts von $\to$ als Zielbereich der Abbildung. Hieraus ergeben sich auch wieder interessante mengentheoretische Aufgaben für dich, wenn Du Mathematik studierst.

Der Kringel $\circ$ ist das mathematische Symbol für die Hintereinanderausführung von zwei Abbildungen. Dabei gilt $(f\circ g) (x) = f(g(x))$ . Die Abbildung rechts vom Kringel, hier g, wird somit zuerst ausgeführt. Ihr Wert ist Argument der linken Abbildung, hier f. Selten wird die Ausführungsreihenfolge von Autoren vertauscht.

Das Symbol für die inverse Abbildung ist das selbe wie für das Urbild. Hier ist jedoch Vorsicht geboten. Beide mathematischen Symbole beschreiben sehr unterschiedliche Dinge.

Das Urbild beschreibt immer eine Menge von Elementen des Definitionsbereichs, die alle auf einen einzelnen Wert im Zielbereich der Abbildung oder auch in eine Teilmenge des Zielbereiches abbilden. Eine einelementige Menge und die leere Menge sind hier nicht ausgeschlossen. Für $f^{-1}(W)=\lbrace x \in D| f(x) \in W\rbrace$ sprichst du: Das Urbild der Menge W unter der Funktion f.

Die inverse Abbildung $f^{-1}$ bildet von einem Element der Zielwerte, $y\in W$ , einer Funktion $f$ auf ein Element der Definitionswerte, $x\in D$ ab. Das heißt, die inverse Abbildung $f^{-1}$ kehrt die Abbildungsvorschrift von $f$ einfach um.

Fazit

Du hast mathematische Symbole zu den Grundlagen, Zahlenmengen, Mengen im Allgemeinen und Abbildungen kennengelernt.

Das sind natürlich bei weitem nicht alle Symbole, die du während deines Studiums brauchen wirst.

Es sind aber die wichtigsten mathematischen Symbole während des ersten Semesters.

Falls du dich umfassender auf dein Mathematikstudium vorbereiten möchtest, erfährst du in dem Artikel Mathematik Studium Vorbereitung: Kenne deine Möglichkeiten welche Themen dabei wichtig für dich sind.

Wenn du Fragen, Anregungen oder Themenwünsche hast, dann schreibe mir eine E-Mail oder hinterlasse dein Anliegen in den Kommentaren.

Anmerkungen, Links und Quellen[+]

Die wichtigsten mathematischen Symbole für dein erstes Studiensemester

Mathematische Symbole – Grundlagen

Mathematische Symbole – Zahlenmengen

Mathematische Symbole – Mengen

Mathematische Symbole – Abbildungen

Fazit

Schreibe einen Kommentar Antworten abbrechen

Mathematische Symbole – Grundlagen

Mathematische Symbole – Zahlenmengen

Mathematische Symbole – Mengen

Mathematische Symbole – Abbildungen

Fazit

Related PostsView more

Mathematik Studium Vorbereitung: Kenne deine Möglichkeiten

Definition-Satz-Beweis – Das System solltest du verstehen

Mathematische Begriffe Teil IV: Kanonisch, i.A., pathologisch

Mathematische Begriffe Teil III: Notwendig, hinreichend, trivial

Mathematische Begriffe Teil II: O.B.d.A., wir, kommutatives Diagramm

Mathematische Begriffe Teil I: Vermöge, oder, wohldefiniert

Schreibe einen Kommentar Antworten abbrechen