Eins plus eins gleich Null | Mathematik Studium Tipps

Eins plus eins gleich null. Was soll das denn? Wohl nicht aufgepasst in der Schule, was?!

Vergiss alles, was du bisher in der Schule gelernt hast! Wir schaffen uns jetzt gemeinsam eine Welt, in der gilt:

1 + 1 = 0 !

Los geht’s!

Der (Zahlen-)Körper im Allgemeinen

Als erstes benötigen wir eine Mengenstruktur, die für uns sicherstellt, dass wir mit den Elementen der Menge (in unserem Fall Zahlen) überhaupt rechnen können. Dafür erwarten wir beispielsweise, dass das Ergebnis einer Rechenoperation auch Element unserer (Zahlen-)Menge ist.

Die Operationen sollen somit nicht aus der Menge herausführen. Man sagt dann auch, die Menge ist abgeschlossen bezüglich der Rechenoperationen.

Weiterhin sollen die Rechenoperationen assoziativ, kommutativ und distributiv sein. Zudem benötigen wir neutrale Elemente und inverse Elemente. Eine Rechenoperation mit dem zugehörigen neutralen Element soll nichts verändern. Eine Rechenoperation eines Elementes mit seinem (ganz persönlichen) inversen Element führt zum neutralen Element der Rechenoperation.

Eine Rechenoperation heißt auch Verknüpfung. Konkreter sehen die Anforderungen an die Menge, deren Elemente wir verknüpfen möchten, so aus:

Eine Menge $K$ mit mindestens zwei Elementen und zwei Verknüpfungen
$+: K \times K,\ (x,y)\mapsto x + y:= +(x,y)$ (Addition)
$\cdot: K \times K,\ (x,y)\mapsto xy:=\cdot(x,y)$ (Multiplikation)
heißt ein Körper (in Zeichen: $(K,+,\cdot)$ ), wenn für alle $x,y,z\in K$ folglende Körperaxiome erfüllt sind:

A – Additionsaxiome

A1: Assoziativgesetz: $x+(y+z) = (x+y) + z$ .
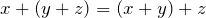A2: Kommutativgesetz: $x+y = y+x$ .
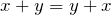A3: Neutrales Element: Es existiert ein Element 0 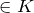$\in K$ mit $x+0=x\ \forall x\in K$ .
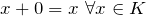A4: Inverse Elemente: 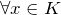$\forall x\in K$ existiert ein Element 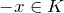$-x\in K$ mit $x + (-x) = 0$ .

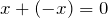M – Multiplikationsaxiome

M1: Assoziativgesetz: $x(yz) = (xy)z$ .
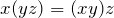M2: Kommutativgesetz: $xy = yx$ .
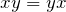M3: Neutrales Element: Es existiert ein Element 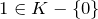$1\in K-\lbrace 0\rbrace$ mit $x1 = x\ \forall x\in K$ .
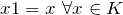M4: Inverse Elemente: 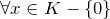$\forall x\in K-\lbrace 0 \rbrace$ existiert ein Element 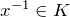$x^{-1}\in K$ mit $xx^{-1}=1$ .

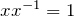D – Distributivgesetz

$x(y+z) = xy + xz = (y+z)x$ .

Beispiele für (Zahlen-)Körper

Die nachfolgenden Beispiele sind dir wahrscheinlich bis auf das Letzte gut bekannt. Beispiel drei ist der Körper der komplexen Zahlen. Du wirst ihn noch in Analysis I kennenlernen.

$(\mathbb{Q},\ +,\ \cdot)$ ist ein Körper mit den neutralen Elementen 0 und 1.
$(\mathbb{R},\ +,\ \cdot)$ ist ein Körper mit den neutralen Elementen 0 und 1.
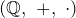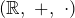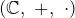$(\mathbb{C},\ +,\ \cdot)$ ist ein Körper mit den neutralen Elementen 0 und 1.

Es gibt noch weitaus mehr Beispiele für Körper, als die Obigen. Du erfährst mehr über Körper in (linearer) Algebra. Wir brauchen für unsere kleine Welt jedoch erst einmal nicht mehr zu wissen.

Unsere Welt, in der 1 + 1 = 0 gilt

Wir schauen uns nun folgende Menge an: $\mathbb{F}_2=\lbrace 0,1\rbrace$ mit $0 \neq 1$ .

Die Menge $\mathbb{F}_2$ ist sogar ein Körper. Das neutrale Element der Addition ist die 0 und das neutrale Element der Multiplikation die 1.

Da $\mathbb{F}_2$ genau zwei Elemente hat, können wir die Behauptung $\mathbb{F}_2$ sei ein Körper ganz einfach überprüfen. Dafür müssen wir nur die Verknüpfungen mit allen Elementen nachrechnen.

Fangen wir mit der Multiplikation an:
$0\cdot 1 = 1\cdot0 = 0$ ,
$1\cdot 1= 1$ ,
$0\cdot 0 = 0$ .

Die Multiplikation ist nicht ungewöhnlich. So kennen wir sie schon aus der Schule. Schauen wir uns nun die Addition an:
$0 + 1 = 1 + 0 = 1$ .
$0 + 0 = 0$ ,
$1 + 1 = 0$ , denn wäre die letzte Gleichung falsch, dann müsste gelten $1 + 1 = 1$ .

Nehmen wir also an, dass $1 + 1 = 1$ ist. Wenn wir dann auf beiden Seiten der Gleichung 1 abziehen¹⁾Hier drücken wir uns etwas ungenau aus. Da -1 nicht Element unserer Menge ist, bedeutet „1 abziehen“ das zu 1 inverse Element addieren. Damit haben wir dann auch eine Null erzeugt., bekommen wir $1 = 0$ . Das ist jedoch ein Widerspruch zu obiger Annahme $1\neq 0$ .

Somit folgt die Behauptung $1 + 1 = 0$ .

Wir haben über die Körperaxiome festgelegt wie die Addition und Multiplikation für eine Menge mit nur zwei Elementen aussieht. Im übrigen ist der $\mathbb{F}_2$ der kleinste Körper und auch der einzige, der nur zwei Elemente hat. Alle anderen Körper mit zwei Elementen lassen sich auf den $\mathbb{F}_2$ zurückführen. Man sagt auch, es gibt bis auf Isomorphie genau einen zweielementigen Körper.

Ein zu $\mathbb{F}_2$ isomorpher Körper ist beispielsweise der Restklassenring $\mathbb{Z} &/ 2\mathbb{Z}=\lbrace a + 2\mathbb{Z}|\ a \in \mathbb{Z} \rbrace=\lbrace 2\mathbb{Z}, 1 + 2\mathbb{Z} \rbrace$ . In dieser Menge werden mit Hilfe der ganzen Zahlen mit $2\mathbb{Z}$ gerade Zahlen und mit $1 + 2\mathbb{Z}$ ungerade Zahlen erzeugt. Dabei bildet $2\mathbb{Z}$ die Restklasse von $2\mathbb{Z}$ modulo 2, also Rest 0. Daher definieren wir $\overline{0}:=2\mathbb{Z}$ . Für $1 + 2\mathbb{Z}$ gilt analog $\overline{1}:=1 + 2\mathbb{Z}$ . Der Strich über der 0 und 1 soll symbolisieren, dass es sich um eine Restklasse handelt.

Die Addition ist im Allgemeinen im Ring $\mathbb{Z} &/ m\mathbb{Z}$ wie folgt definiert: $\overline{a}+\overline{b}=\overline{a+b}=(a+b)+m\mathbb{Z}$ . Die Definition der Multiplikation und die Eindeutigkeit beider Verknüpfungen zeigen wir jetzt mal nicht…