Definition-Satz-Beweis - Das System solltest du verstehen

In den ersten Vorlesungen deines Mathematikstudiums wird dir gleich auffallen, dass ein besonderer Rhythmus im Takt von Definition-Satz-Beweis schlägt.

Nichts erinnert an den Mathematikunterricht in der Schule – wirklich gar nichts!

In der Schule hast du rechnen gelernt. An der Universität lernst du warum du so rechnen durftest und noch weitaus mehr.

Mit der ersten Vorlesung im Mathematikstudium beginnt daher ein Umstellungsprozess.

Für manche ist es auch ein Schock.

Mathematik ist sehr abstrakt und damit ein Grund warum das Mathematikstudium schwer ist.

Zudem ist die mathematische Sprache eine Mischung aus formaler und alltäglicher Sprache. Wörter aus dem Alltag können in der Mathematik eine andere Bedeutung haben, weshalb die Mathematik auch ihre eigenen mathematischen Vokabeln hat.

Definition-Satz-Beweis sind die grundlegendsten und wichtigsten Elemente in deinem Studium. Daher schauen wir sie uns in diesem Beitrag genauer an.

Hast du das System erst einmal verstanden, dann fällt dir das Mathematikstudium gleich etwas leichter.

Das System Definition-Satz-Beweis

Geht es um mathematische Begriffe, und davon lernst du Hunderte in deinem Studium, dann werden sie erst einmal sehr präzise definiert.

Danach werden mit den Begriffen verbundene Eigenschaften und Beziehungen zu anderen mathematischen Objekten untersucht. Die Resultate dieser Untersuchungen lernst du als Mathematikstudent in Form von Sätzen kennen.

Die Sätze werden anschließend bewiesen. Dieser systematische Aufbau der Mathematik wird auch mit „Definition-Satz-Beweis“ beschrieben.

Die gesamte Mathematik ist seit Euklid und seinem Buch „Elemente“ so aufgebaut.

Definitionen

Mathematischen Objekten begegnest du nicht in der U-Bahn, beim Einkaufen oder in der Schlange vor dem Fußballstadion.

Sie sind abstrakt.

Mathematische Objekte gehen über unseren Alltagsverstand hinaus.

Gerade weil wir in unserem Alltag keine Erfahrungen mit mathematischen Objekten machen und uns deshalb keine intuitive Vorstellung darüber bilden können, brauchen wir in der Mathematik Definitionen.

Sehr präzise Definitionen – und zwar für jeden einzelnen mathematischen Begriff.

Daher enstehen regelrechte Kaskaden von aufeinander aufbauenden Begriffen. Es ist nahezu unmöglich einen mathematischen Begriff zu definieren, ohne wieder einen Begriff zu nutzen, der einer Definition bedarf.

Erst mit einem ausreichend großen Vorrat an Definitionen lässt sich Mathematik erklären und schließlich auch verstehen. Eine einfache Erklärung eines mathematischen Zusammenhangs ist i.d.R. unmöglich. Schon Euklid wußte: Es gibt keinen Königsweg zur Mathematik.¹⁾Greuel, G.-M. (2011): Mathematik zwischen Forschung, Anwendung und Vermittlung, Universität Kaiserslautern.

Die erste Definition aus Euklids „Elemente“ lautet:

Was keine Teile hat, ist ein Punkt.

Da es die erste Definition von Euklid ist, setzt er somit voraus, dass der Leser weiß, was ein Teil ist.

Zwar weiß auch jeder aus dem Grammatikunterricht was ein Punkt ist, doch Vorsicht! Hier ist nicht der Punkt aus unserem Alltag gemeint.

Wir sprechen von einem mathematischen Objekt, das Punkt genannt wurde.

Grundsätzlich geht es auch nicht darum, zu verstehen was mathematische Objekte sind, sondern vielmehr in welcher Beziehung sie zueinander stehen.

Bleiben wir doch in der Geometrie:

Zwei Punkte bestimmen eine Gerade.

Damit haben wir zwar nicht direkt gesagt, was eine Gerade ist. Aber darauf kommt es ja auch nicht an!

Gewöhnungsbedürftig? Ja, das stimmt.

Mal ein ganz anderes Beispiel

Vielleicht hilft ein Beispiel, was verdeutlichen soll, dass es keiner Dinglichkeit bedarf. Allein auf die logische Struktur kommt es an:²⁾Fritzsche, K. (2007): Mathematik für Einsteiger, Vor- und Brückenkurs zum Studienbeginn, 4. Auflage, München. Zweistein (1967): Logeleien, in: Die Zeit, 24.11.1967.

Alle Knaffs haben die gleiche Form und sind gleich groß.

Alle grünen Hunkis haben ebenfalls die gleiche Form und Größe.

Zwanzig Knaffs passen gerade in einem Plauz.

Alle Hemputis enthalten grüne Hunkis.

Ein grüner Hunki ist zehn Prozent größer als ein Knaff.

Ein Hemputi ist kleiner als ein Plauz.

Wenn der Inhalt aller Plauze und aller Hemputis vorwiegend rot ist, wie viele grüne Hunkis könnnen maximal in einem Hemputi sein?

Für die Lösung klicke einfach auf die Fußnote.³⁾Es können maximal 8 grüne Hunkis in einem Hempti sein.

Axiome und Sätze

Mathematische Aussagen beschreiben Beziehungen zwischen mathematischen Objekten. Somit haben sie per Definition einen Wahrheitswert.

Eine mathematische Aussage hat per Definition stets einen Wahrheitswert.

Beides, Axiome und Sätze, sind mathematische Aussagen. Der Unterschied zwischen ihnen liegt darin, dass Axiome nicht bewiesen werden. Sie werden ähnlich wie Spielregeln anerkannt und gelten auch als allgemeine, unzweifelbare Grundsätze. ⁴⁾Beetz, J. (2013): 1 + 1 = 10, Mathematik für Höhlenmenschen, Berlin.

Das Axiomensystem

Ein Axiom kommt jedoch selten allein. Vor jeder Theorie steht ein ganzes System von Axiomen. Das Axiomensystem muss vollständig, unabhängig und widerspruchsfrei sein. Es bildet die Basis für alle daraus abgeleiteten Sätze. Daher ist jeder dieser Sätze auch lediglich relativ wahr.⁵⁾Fritzsche, K. (2007): Mathematik für Einsteiger, Vor- und Brückenkurs zum Studienbeginn, 4. Auflage, München.

Ein Beispiel für ein Axiomensystem, dem noch eine Definition vorangestellt ist, ist Folgendes:

Definition: Eine Menge $K$ mit mindestens zwei Elementen und zwei Verknüpfungen
$+:\ K\times K \to K,\quad (x,y)\mapsto x + y:= +(x,y)$ (Addition) und
$\cdot :\ K\times K \to K,\quad (x,y)\mapsto xy:=\cdot (x,y)$ (Multiplikation)
heißt ein Körper (in Zeichen: $(K,+,\cdot)$ ), wenn für alle $x,y,z\in K$ die folgenden Körperaxiome erfüllt sind:

Axiome der Addition

A1: Assoziativgesetz: $x + (y + z) = (x + y) + z$
A2: Kommutativgesetz: $x + y = y + x$
A3: Exitenz der Null: Es existiert ein Element $0\in K$ mit $x + 0 = x$ für alle $x\in K$ .
A4: Existenz des Negativen: Für alle $x\in K$ existiert ein Element $-x\in K$ mit $x + (-x) = 0$ .

Axiome der Multiplikation

M1: Assoziativgesetz: $x(yz) = (xy)z$
M2: Kommutativgesetz: $xy = yx$
M3: Exitenz der Eins: Es existiert ein Element $1\in K\setminus \lbrace 0 \rbrace$ mit $x1 = x$ für alle $x\in K$ .
M4: Existenz des Inversen: Für alle $x\in K\setminus \lbrace 0 \rbrace$ existiert ein Element $x^{-1}\in K$ mit $xx^{-1} = 1$ .

Distributivgesetz: $x(y + z) = xy + xz = (y + z) x$

Daraus lässt sich auch gleich ein erster Satz ableiten:

Satz: Seien $x,y\in K$ . Die Gleichung $x+z=y$ hat die eindeutig bestimmte Lösung $z=y-x \in K$ .

Natürlich ist ein Satz auch erst ein Satz, wenn er bewiesen wurde. Das machen wir in diesem Beitrag jedoch nicht.

Zunächst noch ein paar Worte zum Aufbau von Sätzen und ihrem Hierarchiesystem.

Der Aufbau von Sätzen

In jedem mathematiscchen Satz werden zu Beginn die Voraussetzungen vorgestellt. Darunter fällt die Vorstellung der mathematischen Objekte, ihrer Eigenschaften und gegebenenfalls auch ihrer Beziehungen, in der sie zueinander stehen. Genauso gut können Sätze auch Definitionen enthalten.

Erst nachdem alle Voraussetzungen klar sind, folgt die Behauptung. In Bezug auf unseren obigen Satz sind die Voraussetzungen in „Seien $x,y\in K$ .“ zusammengefasst. Der darauf folgende Teil „Die Gleichung $x+z=y$ hat die eindeutig bestimmte Lösung $z=y-x \in K$ .“ ist die Behauptung.

Sobald die Aussage bewiesen wurde, ergeben Voraussetzung und Behauptung samt Beweis einen mathematischen Satz.

Unbewiesene Aussagen sind Vermutungen oder auch Behauptungen. Ihr Wahrheitswert ist somit noch unbekannt. Zu den bekanntesten Vermutungen zählen die Fermatsche Vermutung, die mittlerweile keine mehr ist, und die Goldbachsche Vermutung.

Das Hierarchiesystem mathematischer Sätze

Nicht jeder mathematische Satz ist gleich wichtig. Es gibt drei Kategorien, die gleichzeitig Auskunft über die hierarchische Stellung einer mathematischen Aussage geben.

Wir unterscheiden zwischen

Theorem, auch Hauptsatz genannt.
Korollar, ein Folgesatz.
Lemma, auch als Hilfssatz bekannt.

Ein Theorem, oder auch Hauptsatz, zeichnet sich dadurch aus, dass er das Kernstück einer Theorie ist. Er ist von großer Bedeutung und Reichweite.

Das nachfolgende Beispiel stammt aus der Analysis I:

Hauptsatz der Differential- und Integralrechnung: Ist $f\in C(I)$ uund $F$ Stammfunktion von $f$ , so gilt für alle $a,b\in I$

$\begin{align*} \int_{a}^{b} f(x)dx = F(x)|_{a}^{b}:=F(b)-F(a). \end{align*}$

Ein Korollar dagegen ist eine unmittelbare, fast schon triviale, Folgerung aus einem Hauptsatz. Sie braucht daher nicht zwingend bewiesen werden. Das gilt vor allem in der Vorlesung. 🙂 Typischerweise erteilt die Professorin oder der Professor den Beweis dann als Hausaufgabe.

Ein Beispiel aus der Linearen Algebra I mit vorangestellten Satz lautet:

Satz: Es sei $V$ ein endlich dimensionaler Vektorraum.

Eine linear unabhängige Menge in 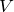$V$ kann zu einer Basis erweitert werden, in dem man weitere Vektoren hinzufügt.
Jede Menge von Vektoren, die 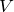$V$ aufspannt, kann durch eventuelles Weglassen von Vekktoren zu einer Basis gemacht werden.

Korollar: Es sei $V$ ein Vektorraum der Dimension $n$ . Dann gelten:

Jede Menge von 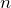$n$ Vektoren, die 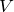$V$ aufspannt, ist eine Basis von $V$ .
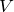Jede Menge von 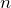$n$ linear unabhängigen Vektoren aus 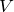$V$ ist eine Basis von $V$ .

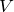Ein Lemma hat den niedrigsten Rang in der Hierarchie. Es ist ein Hilfssatz. Hilfsätze sind nützlich, da sie beispielsweise vorbereitende Arbeit für einen Hauptsatz leisten. Obwohl sie lediglich eine Hilfsaufgabe haben, gibt es Lemmata, die genauso bedeutend sind wie Hauptsätze.

Hier ist ein sehr bekanntes Beispiel aus der Mengenlehre:

Lemma von Zorn: Eine halbgeordnete Menge, in der jede Kette eine obere Schranke hat, enthält mindestens ein maximales Element.

Für alle obigen Sätze sind die Beweise bewußt ausgelassen worden.

Nicht jeder Satz muss in eine der Kategorien eingeordnet werden. Es gibt auch kategorieunabhängige Sätze. Die erkennst du daran, dass sie dann auch einfach nur „Satz“ heißen.

Generell gilt:

Eine mathematische Aussage, die den Namen eines Mathematikers trägt, ist wichtig.

Beweise

Das Thema Beweis aus dem System Definition-Satz-Beweis ist das komplexeste Thema. Das liegt vor allem daran, dass es für einen Beweis kein Patentrezept gibt.

Auch wenn Beweise den Gesetzen der Logik folgen, ist es oft nicht so leicht die Lücke zwischen einer Voraussetzung $A$ und einer Behauptung $B$ zu schließen.

Gelegentlich spricht man auch von der Kunst des Schlussfolgerns, wenn es um das Beweisen geht.

Trotzdem gibt es so etwas wie Beweistypen.

Sie können für sich schon ausreichend sein, um eine Aussage zu beweisen.

Um so weiter du in der Mathematik fortschreitest, desto eher bestehen die Beweise aus einer Mischung von verschiedenen Typen.

Die Beweistypen

Wahrscheinlich würde hier die Nennung von nur zwei Typen ausreichen, da sich weitere Beweistypen daraus konstruieren ließen. Sagen wir mal die folgenden beiden Beweistypen sind die Urtypen:

Direkter Beweis
Induktionsbeweis

Eine Sammlung einiger Beweistypen zeigt die nachfolgende Grafik.

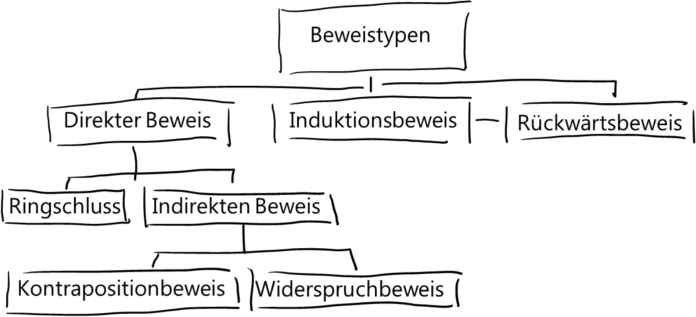
Der direkte Beweis und seine Verwandtschaft

Der direkte Beweis ist das, was seine Bezeichnung schon sagt. Du startest mit der Voraussetzung $A$ und folgerst über andere bereits bewiesene Aussagen so lange bis du dein Ziel, die Behauptung $B$ , erreicht hast.

Eine Spezialität des direkten Beweises ist der Ringschluss. Er zeichnet sich durch eine Kette von direkten Beweisen aus, die dadurch, dass aus dem Ende der Kette auch wieder der Anfang der Kette gefolgert werden kann, ein Ring entsteht.

Typischerweise wird im Satz eine Äquivalenz von mindestens drei Aussagen behauptet: $A\Leftrightarrow B\Leftrightarrow C$ .

Der Ringschluss funktioniert dann so: $A\Rightarrow B\Rightarrow C\Rightarrow A$ . Die Rückrichtung ist durch den Schluss von $C\Rightarrow A$ implizit gegeben.

Der indirekte Beweis funktioniert „irgendwie“ hintenrum. Beim Kontrapositonbeweis bedeutet hintenrum, dass zunächst eine äquivalente Aussage auf dem direkten Wege bewiesen wird. Wegen der Äquivalenz (das heißt Gleichwertigkeit) kann dann auf den Wahrheitsgehalt der ursprünglichen Aussage geschlossen werden:

$(A\Rightarrow B) \Leftrightarrow (\neg B \Rightarrow \neg A)$ .

Der Widerspruchbeweis funktioniert auch hintenrum. Denn zu Beginn wird einfach angenommen, dass die zu beweisende Aussage $A$ nicht wahr ist, $\neg A$ . Daraufhin folgt so lange eine direkte Kette von Aussagen, bis es einen Widerspruch zum Anfang gibt:

$A \wedge \neg A$ .

Der Induktionsbeweis und der Rückwärtsbeweis

Der Induktionsbeweis eignet sich für Aussagen, bei denen eine Aussage $E(x)$ für alle natürlichen Zahlen bewiesen werden muss.

Das Prinzip der vollständigen Induktion beruht auf dem 5. Axiom von Peano. Er charakterisiert mit fünf Axiomen die natürlichen Zahlen. Das 5. Axiom lautet:

$\forall E(x):\ (E(1) \wedge \forall\ n\in\mathbb{N}:\ (E(n)\Rightarrow E(n+1)) \Rightarrow (\forall\ n\in \mathbb{N}:\ E(n)).$

Basierend auf diesem Axiom läuft der Beweis dann immer nach dem selben Schema ab. Dafür gibt es im Grunde ein Vorlage, die wir hier jedoch nicht behandeln.

Der Rückwärtsbeweis hat in kleinen Teilen Ähnlichkeit zur Induktion. Bei der Induktion wird nach ein wenig Vorarbeit von $E(n)$ auf $E(n+1)$ geschlossen. Da wir durchaus wissen wie $E(n+1)$ aussieht, wird „dort hin gerechnet“.

Beim Rückwärtsbeweis ist die Zielformel bereits bekannt, da sie die Behauptung ist. Mit diesem Wissen wird zurück auf die Voraussetzungen gerechnet.

Nicht aufgeführt sind der Existenzbeweis und der Eindeutigkeitsbeweis. Sie sollen aber wenigstens Erwähnung finden.

Über Beweise lässt sich noch jede Menge mehr sagen. Im Kontext von Definition-Satz-Beweis soll dieser kleine Überblick erst einmal ausreichen.

Zu guter Letzt sollte dir noch kar sein, dass es stets mehr als einen Beweis für ein und die selbe mathematische Aussage gibt.

Fazit

In deinem Mathematikstudium dreht sich alles um Definition-Satz-Beweis.

Definitionen beschreiben ein mathematisches Objekt. Es ist nicht notwendig sich ein Bild davon zu machen, was die Definitionen beschreiben. Von Begriffen, die du bereits aus dem Alltag kennst, solltest du dich frei machen. In der Mathematik bedeuten sie höchst wahrscheinlich etwas Anderes.

Ein mathematischer Satz nennt Beziehungen zwischen oder Eigenschaften von mathematischen Objekten. Er lässt sich theoretisch bis auf die Axiome, welches die Grundaussagen sind, zurückführen. Praktisch wird ein Beweis dann viel zu lang.

Der Beweis hat die Aufgabe, die Beziehungen oder Eigenschaften nachvollziehbar mit Hilfe weiterer mathematischer Aussagen aufzudecken. Eine logische Argumentationskette entsteht. Sie erklärt warum die im Satz behauptete Beziehung wahr ist.

Hast du den Aufbau und die Bedeutung des Systems Definition-Satz-Beweis verstanden, dann bist du auf dem besten Weg auch Teile der Mathematik zu verstehen.

[newsletterBox]

Anmerkungen, Links und Quellen[+]

Anmerkungen, Links und Quellen
↩1	Greuel, G.-M. (2011): Mathematik zwischen Forschung, Anwendung und Vermittlung, Universität Kaiserslautern.
↩2	Fritzsche, K. (2007): Mathematik für Einsteiger, Vor- und Brückenkurs zum Studienbeginn, 4. Auflage, München. Zweistein (1967): Logeleien, in: Die Zeit, 24.11.1967.
↩3	Es können maximal 8 grüne Hunkis in einem Hempti sein.
↩4	Beetz, J. (2013): 1 + 1 = 10, Mathematik für Höhlenmenschen, Berlin.
↩5	Fritzsche, K. (2007): Mathematik für Einsteiger, Vor- und Brückenkurs zum Studienbeginn, 4. Auflage, München.

2 Kommentare Neues Kommentar hinzufügen

Christine sagt:

„Eine mathematische Aussage ist per Definition stets wahr.“
Das ist falsch! Eine Aussage kann wahr oder falsch sein. Ein Satz ist eine wahre Aussage. Bitte nicht verwechseln!

25. Mai 2018 um 15:54
Antworten
1. Liane sagt:
  
  Hallo Christine,
  
  na klar, du hast Recht! Es muss natürlich heißen: „Eine mathematische Aussage hat per Definition stets einen Wahrheitswert.“
  
  Vielen lieben Dank für den Hinweis.
  Liane
  
  25. Mai 2018 um 19:37
  Antworten

Definition-Satz-Beweis – Das System solltest du verstehen

Das System Definition-Satz-Beweis